|
Равноускоренным называют движение с постоянным ускорением. Простейшим примером такого движения является свободное падение тел, изучением которых занимался ещё Галилео Галилей. Скорость движения при этом не остаётся постоянной: в общем случае она меняется и по модулю, и по направлению. Описание данного движения значительно сложнее по сравнению с равномерным прямолинейном. Действия с числами здесь заменяют на действия с векторами, так как векторы содержат в себе информацию о направлений величин, характеризующих движение (о скорости, ускорений, перемещений).
Ускорение при равноускоренном движений показывает, на сколько изменяется скорость тела за каждую секунду движения:
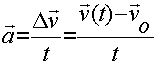 (1) (1)
Где V0 – начальная скорость тела, а V скорость того же тела спустя некоторое время t.
Ускорение показывает изменение скорости за единицу времени.
Из определения ускорения следует, что мгновенная скорость тела при равноускоренном движении изменяется с течением времени по линейному закону:
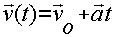 (2) (2)
Эта формула позволяет по начальной скорости и ускорению тела вычислить его скорость в любой момент времени t.
Между тем основная задача механики заключается в определении того, где будет находиться тело спустя заданное время. Для её решения необходимо знать перемещение, совершённое телом за это время. Перемещение можно найти, умножив среднюю скорость на время движения:
s=vcpt
При равноускоренном движении средняя скорость равна полусумме начальной и конечной скоростей движения:
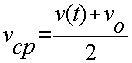
Поэтому:
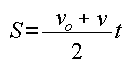
Подставляя сюда выражения (2), получаем:
s=v0t +at2/2(3)
Именно это уравнение является обобщением формулы:s=vt на случай движения с постоянным ускорением.
Уравнения (1),(2),(3) – векторные. Действия с векторами отличаются от действий с числами, поэтому никакие числовые значения перемещения, скорости и ускорения в такие уравнения подставлять нельзя. Между тем любые расчёты требуют проведений операций именно с числами. Чтобы это стало возможным, необходимо от векторного способа описания движения перейти к координатному.
При координатном описаний движения вместо векторов используют проекций на оси координат. Поскольку любой вектор характеризуется тремя проекциями на оси X,Y и Z, следовательно каждому вектору уравнению в общем случае будут соответствовать три уравнения в координатной форме.
Для плоского (двухмерного) движения таких уравнений только два. Если же движение является прямолинейным, то для его описания достаточно одного уравнения в проекций на ось X(при условии, что эта ось направлена параллельно вектору скорости частицы). Тогда уравнения (2) и (3).например, можно записать следующим образом:
vx=v0x+axt
sx=v0xt+axt2/2(4)
При координатном описаний движения, координота тела будет равна:
x=x0+v0xt+axt2/2(5)
|



